Ο πίνακας MATRIX ως τρόπος εκμάθησης μελωδικών διαστημάτων [tip #7]
Nov 8, 2014Στο tip #2 “6 Βασικές Χρήσεις της Χρωματικής Κλίμακας στη Θεωρία Μουσικής”, εξηγήθηκε με συνοπτικό τρόπο η σημασία της και η χρησιμότητά της στην εκμάθηση βασικότατων κεφαλαίων της θεωρίας της μουσικής.
Σε αυτό το tip θα επικεντρώσω περισσότερο στον υπολογισμό των μελωδικών διαστημάτων με βάση το ημιτόνιο (12 χρωματικές βαθμίδες).
Διευκρίνηση: Σε καμία περίπτωση (αυτό) δεν αποτελεί εισαγωγή στις κατεξοχήν τεχνικές του δωδεκαφθογγισμού και στην κατανόηση των κύριων εννοιών του, αλλά αντίθετα χρησιμοποιεί ορισμένα στοιχεία από την αυστηρή οργάνωση των δωδεκάφθογγων σειρών, προκειμένου να αποτελέσει έναν γρήγορο και αποτελεσματικό τρόπο μελέτης των μελωδικών διαστημάτων.
Τα αποτελέσματα που έχω στην διάθεσή μου δείχνουν ότι, μαθητές που έμαθαν να χρησιμοποιούν και να κατανοούν την λειτουργία της χρωματικής σκάλας από την αρχή των σπουδών τους (συγκεκριμένα από την στιγμή που εμφανίζονται οι πρώτες αλλοιώσεις στα μουσικά κομμάτια που εκτελούν στα όργανα), δεν αντιμετωπίζουν πρόβλημα υπολογισμού των διαστημάτων και οι πιθανότητες λάθους είναι ελάχιστες.
Η εκπαίδευση στα ημιτόνια της χρωματικής είναι πολύ λιγότερο χρονοβόρα από οποιαδήποτε άλλη μέθοδο. Αρκεί να μπορεί ο δάσκαλος να δώσει κατευθύνσεις με τον συντομότερο και καλύτερο δυνατό τρόπο.
Πιο συγκεκριμένα, η αναγνώριση μελωδικών διαστημάτων με βάση τον αριθμό των ημιτονίων που περιέχουν (η 1η Καθαρή αντιστοιχεί σε 0 ημιτόνια, η 2η μικρή σε 1 ημ., η 2η Μεγάλη σε 2 ημ. κοκ. 1) οριοθετείται στο διάστημα της 5ης Καθαρής που αντιστοιχεί σε 7 ημ. (κύκλος των 5ων όπου οι μεταφορές του προτύπου ταξινομούνται κατά 5ες Καθαρές).
Όλα τα μεγαλύτερα σε απόσταση μελωδικά διαστήματα αναγνωρίζονται με βάση τα συμπληρωματικά τους (ανεστραμμένα) διαστήματα πχ.C-A (6η Μ) = Α-C (3η μ), F#-Eb (7η ελ) = Eb-F# (2η Αυξ) κλπ.
Αυτός ο τρόπος αναγνώρισης είναι μια διαδικασία διπλής κατεύθυνσης, δηλ. οδηγεί πολύ εύκολα στις βασικές αρχές της ατονικής μουσικής ( σχηματισμός πίνακα MATRIX με τις δωδεκάφθογγες σειρές), αλλά και αντιστρόφως ο ίδιος ο πίνακας μπορεί να χρησιμεύσει ως παιχνίδι για:
- την εκμάθηση των διαστημάτων,
- τις μεταφορές τους σε οποιαδήποτε χρωματική βαθμίδα και
- για το “συντακτικό” της μουσικής γραφής πχ. κανονική μορφή μιας ομάδας φθόγγων (prime), αντίθετη μορφή (inversion), καρκινική μορφή (rertrograde) και καρκινική της ανεστραμμένης μορφής (retrograde inversion).
Έτσι λοιπόν, ορίζοντας μια δωδεκάφθογγη διαδοχή που δεν χρειάζεται να πληροί τους αυστηρούς νόμους του δωδεκαφθογγισμού σύμφωνα με τον A. Schönberg, μπορούμε να έχουμε:

Η νέα μορφή της σειράς απεικονίζει τους φθόγγους της αρχικής σειράς σε ανοδική διάταξη (από τoν φθόγγο E):

Η παραπάνω διάταξη μπορεί να τοποθετηθεί μέσα στον πίνακα MATRIX (“magic square”) που είναι ένα σύστημα με γραμμές και στήλες, ως εξής:
Οριζοντίως, από την θέση P0 τοποθετούμε τους 12 φθόγγους της σειράς, συμβολίζοντάς τους με την σημειογραφία A, B, C, D κλπ.
Η κάθετη στήλη ξεκινάει πάλι με τον αρχικό φθόγγο της σειράς (Ε), στην θέση I0, αλλά όλα τα υπόλοιπα νούμερα (αριθμός ημιτονίων) προκύπτουν ως διαφορά εάν αφαιρέσουμε από τα 12 ημιτόνια της χρωματικής σκάλας,τα ημιτόνια της αρχικής σειράς:
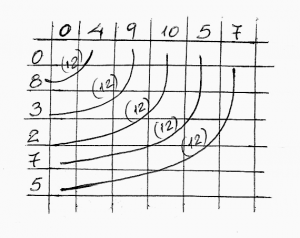
Οι φθόγγοι που βρίσκονται στην αρχή κάθε γραμμής πχ. P8©, P3(G), P2(F#), P7(B), P5(Α), P11(Eb) κλπ., είναι στην πραγματικότητα ένα συνεχές transporto (μεταφορά της αρχικής σειράς) από όλες τις χρωματικές βαθμίδες.
Τα υπόλοιπα διαστήματα υπολογίζονται κάθε φορά από τη νέα αφετηρία.
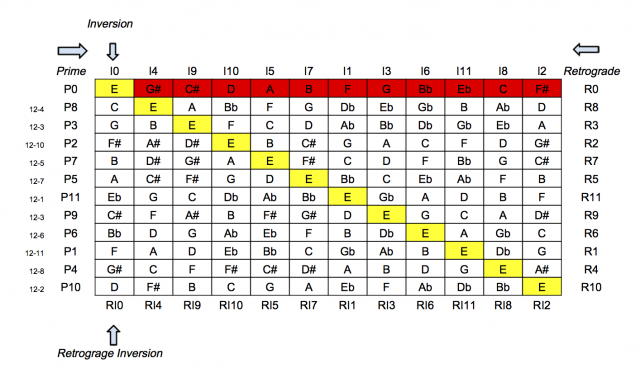
Η διαδικασία είναι αρκετά χρήσιμη για την κατασκευή διαστημάτων από οποιαδήποτε βαθμίδα, καθώς και για τον χειρισμό των εναρμονίων αλλαγών, χωρίς να μεταβάλλεται το περιεχόμενο δηλαδή ο αριθμός των ημιτονίων σε κάθε μελωδικό διάστημα.
Επιπλέον, η κάθε οριζόντια γραμμή μπορεί να διαβαστεί από αριστερά προς τα δεξιά:
Πρωταρχική μορφή της σειράς ➡️ Prime form, (P0, P8, P3 κλπ.)

ή ανάποδα, από δεξιά προς αριστερά:
Καρκινική μορφή ⬅️ Retrograde (R0, R8, R3 κλπ.).

Η κάθετη στήλη διαβάζεται είτε από πάνω προς τα κάτω:
Ανεστραμμένη μορφή ή κατοπτρική της αρχικής σειράς ⬇️ Inversion (I0, I4, I9 κλπ.)
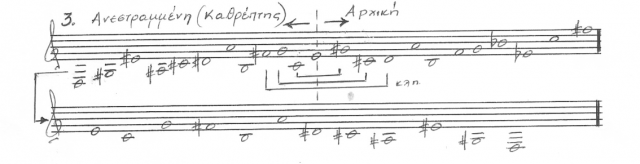
είτε ανάποδα από κάτω προς τα επάνω:
Καρκινική της ανεστραμμένης μορφής ⬆️ Retrograde Inversion (RI0, RI4, RI9 κλπ.)2

Οι μορφές αυτές είναι ορισμένοι (όχι οι μοναδικοί) από τους πιο χαρακτηριστικούς τρόπους παρουσίασης μιας ομάδας φθόγγων (όχι απαραίτητα 12 φθόγγων) που συνθέτουν μια οποιαδήποτε μελωδική γραμμή και συναντώνται στην πλειοψηφία των μουσικών έργων.
Ο τελικός στόχος όλων των παραπάνω είναι να κατανοήσει ο σπουδαστής μουσικής ότι τα μελωδικά διαστήματα είναι από τους ελάχιστους καθοριστικούς παράγοντες που μπορούν να δημιουργήσουν μεγαλύτερες μουσικές δομές, ενώ ο τρόπος χειρισμού τους μπορεί να οδηγήσει σε ενδιαφέροντα ή μη, μουσικά αποτελέσματα.
Επιπλέον, οι μορφές με τις οποίες εμφανίζονται οι γραμμές και οι στήλες καθώς και το φθογγικό υλικό που περιέχουν, προσφέρει πάρα πολλές δυνατότητες συνδυασμών σε όποιον θα επιθυμούσε να το χρησιμοποιήσει στην σύνθεση μουσικής.