Ρυθμός, 3 βασικά ζητήματα [Tip #8]

Oct 30, 2015

Στο σημερινό tip αναφέρομαι σε 3 βασικά ζητήματα, για να ξεκινήσει κάποιος να ακούει σωστά, ώστε να παίζει σωστά.

• Χρονικές διάρκειες.

• Ενδείξεις μέτρων.

• Υποδιαιρέσεις του βασικού χτύπου – Tempo και μετρονόμος.

Η σύγχυση που επικρατεί σχετικά με τα παραπάνω ζητήματα, τόσο στους μαθητές, όσο και σε ένα ποσοστό διδασκόντων είναι ανησυχητικά μεγάλη.

Για παράδειγμα η ένδειξη μέτρου ⁴⁄₄ = 4/♩ έχει παγιωθεί στο μυαλό των περισσοτέρων ως κλάσμα (ορισμένοι το ονομάζουν και μουσικό κλάσμα, για να το διαχωρίσουν από το αριθμητικό κλάσμα) με κλασματική γραμμή, η οποία όπως – εξωφρενικά – διδάσκονται δεν φαίνεται στις παρτιτούρες γιατί “την κρύβει η 3η γραμμή του πενταγράμμου!”. Ακόμη πιο εξωφρενικά ότι “η 3η γραμμή του πενταγράμμου παίζει τον ρόλο της χαμένης(!!) κλασματικής γραμμής!!!”. Έχω διαπιστώσει ότι αυτό το τελευταίο τείνει να το υιοθετήσει το μεγαλύτερο ποσοστό των μαθητών. Τι επικρατεί στο μυαλό όσων διδάσκουν τέτοια πράγματα;

Μέσα από την προσωπική μου εμπειρία θεωρώ ότι, το να δώσει κάποιος έναν ορισμό σχετικά με τον ρυθμό από νωρίς – ιδιαίτερα στους αρχάριους μαθητές του -, είναι μάλλον επιπόλαιο.

Καλύτερα να ξεκινήσει από τα επιμέρους στοιχεία αυτού που ονομάζουμε ρυθμό (κίνηση μέσα στον χρόνο). Έτσι αποφεύγει αστοχίες και “παρεξηγήσεις” του τύπου: “παίξε σε πιο γρήγορο ρυθμό” (εννοεί: tempo, δηλαδή ταχύτητα του χτύπου ή “παίξε σε ρυθμό ²⁄₄” (εννοεί: υπολόγισε 2 χτύπους ανά μέτρο). Γι’ αυτό είναι καλό να υπάρχει απόλυτη σαφήνεια με αυτές τις έννοιες.

Χρονικές διάρκειες (time values)

Σχετικά με το 1ο θέμα που αφορά τις αξίες των φθογγοσήμων (χρονικές διάρκειες), το ζητούμενο δεν είναι απλά να δείξουμε ότι το ολόκληρο = 4 χρόνοι, το μισό = 2 χρόνοι κλπ. (κατά τη γνωστή συνήθεια). Είναι να αντιληφθεί ο κάθε μαθητής , από τον μικρότερο ως τον μεγαλύτερο, ότι την κίνηση πάντα την δίνει ο 1 χτύπος ή βήμα και για αρχή θα αντιστοιχίσουμε αυτόν τον χτύπο με την αξία του τετάρτου¹

Με βάση πάντα τον κεντρικό χτύπο, υπολογίζουμε αντίστοιχα συντομότερες (μικρά βήματα) χρονικά αξίες (όγδοα και δέκατα έκτα) ή στατικές αξίες (σταμάτημα της κίνησης), όπως ολόκληρα, μισά, κλπ.

Συμβαίνει συχνά να κρατούν τα παιδιά ατελείωτους πίνακες του τύπου:

ολόκληρο = 4

μισό = 2

τέταρτο = 1

όγδοο = ¹⁄₂

δέκατο έκτο = ¹⁄₄

τριακοστό δεύτερο = ¹⁄₈

εξηκοστό τέταρτο = ¹⁄₁₆

χωρίς την πραγματική αναφορά σε ένδειξη μέτρου(!) δηλ. ποιες είναι οι προϋποθέσεις ώστε όλες οι αξίες να διαρκούν όσο δείχνει ο πίνακας.

Όλο το σύστημα του υπολογισμού των αξιών δεν είναι απλή απομνημόνευση ενός πίνακα αλλά μια δυναμική διαδικασία που οδηγεί μέσα από πολλά ρυθμικά παιχνίδια στην κατανόηση των αναλογιών.

Ενδείξεις μέτρων (time signatures)

Τo 2ο ζήτημα που αφορά τις ενδείξεις μέτρων έρχεται να συμπληρώσει όλα τα παραπάνω, μόνον εφόσον εξηγηθεί με τον πραγματικό ρόλο που παίζει.

Έχουν πέσει στην αντίληψή μου επεξηγήσεις των ενδείξεων μέτρων ως εξής:

⁴⁄₄ = 4/τέταρτα, ⁶⁄₈ = 6/όγδοα, ³⁄₂ = 3/δεύτερα .

Κατά την γνώμη μου και σύμφωνα με τον τρόπο που διδάσκω εδώ και χρόνια, είναι ο αποτελεσματικότερος τρόπος, για να κατανοηθεί ποια αξία μπαίνει στην θέση του ενός (1) χτύπου κάθε φορά.

Έτσι στο ⁴⁄₄ = 4/τέταρτα το τέταρτο είναι ο 1 χτύπος (άρα 1 χρόνος),

στο ⁶⁄₈ = 6/όγδοα το όγδοο είναι ο 1 χτύπος (άρα 1 χρόνος),

στο ³⁄₂ = 3/δεύτερα το μισό είναι ο 1 χτύπος (άρα 1 χρόνος).

Εάν γίνει ξεκάθαρη η λειτουργία της ένδειξης μέτρου, η οποία πρέπει να επισημαίνεται διαρκώς με κάθε ευκαιρία, ο μαθητής έχει ξεκλειδώσει ένα σημαντικό κεφάλαιο της ρυθμικής του εκπαίδευσης.

Υποδιαιρέσεις του βασικού χτύπου (divisions)

Το 3ο ζήτημα αφορά τις διαιρέσεις του κεντρικού (βασικού) χτύπου κάθε φορά όπως ορίζεται στις ενδείξεις μέτρων.

Έτσι, για παράδειγμα η ένδειξη μέτρου ³⁄₄ μας δείχνει ότι θα μετρήσουμε 3 χτύπους που θα είναι ίσοι με 3 τέταρτα ή με οποιονδήποτε συνδυασμό αξιών και παύσεων που η συνολική τους διάρκεια θα είναι ίση με 3 τέταρτα δηλ.

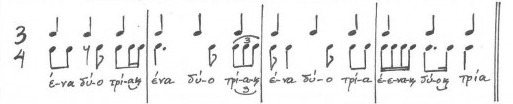
Σε οποιεσδήποτε διαιρέσεις του βασικού χτύπου προκύπτει ένα άλλο σημαντικό θέμα, το 8tempo, δηλαδή πόσο σταθερά θα λέμε με την φωνή μας τους 3 χτύπους, είτε σε αργή, είτε σε μέτρια , είτε σε γρήγορη ταχύτητα με τις όποιες διαιρέσεις προκύπτουν.

Κι΄ενώ η χρήση του μετρονόμου φαίνεται ότι λύνει το πρόβλημα της σταθερότητας του χτύπου, δεν λύνει με τίποτα το πρόβλημα της διαίρεσής του².

Στην πραγματικότητα ο μετρονόμος δεν λύνει ούτε το πρόβλημα της σταθερότητας του χτύπου. Ο πιο σίγουρος τρόπος είναι η διαρκής συνεργασία καλά εκπαιδευμένου δασκάλου και μαθητή, ώστε να επιτευχθεί ο συγκεκριμένος στόχος.

Από την πλευρά του διδάσκοντος απαιτείται η καλή γνώση, η επιμονή και η ανακάλυψη του τρόπου για να το κατανοήσει κάθε μαθητής του.

Από την άλλη πλευρά, του μαθητή, χρειάζεται πολλή ενασχόληση, υπομονή και διαρκείς ερωτήσεις για διάφορα προβλήματα που θα προκύψουν.

Είναι αρκετά συνηθισμένο το φαινόμενο παιδιών που δεν γνωρίζουν τι σημαίνει, μετράω σταθερά, μετράω φωναχτά με συγκεκριμένες συλλαβές για κάθε μία από τις διαιρέσεις (βλ. παράδειγμα), μετράω αλλάζοντας το tempo χωρίς να αλλοιώνω τις διαιρέσεις του χτύπου, γενικά μετράω με συνέπεια για όσα χρόνια παίζω μουσική, ώστε η χρήση του μετρονόμου να βελτιώνει πραγματικά την εκτέλεση και όχι να προσθέτει ακόμη μεγαλύτερα προβλήματα σε αυτή.

Ο μετρονόμος δεν εκπαιδεύει. Ο δάσκαλος εκπαιδεύει.

Ο μετρονόμος βελτιώνει τον ήδη ρυθμικά εκπαιδευμένο και εκπαιδευόμενο σπουδαστή μουσικής._

Η τελευταία παράγραφος απευθύνεται στους γονείς. Εάν (κυρίως) στα χρόνια της βασικής εκπαίδευσης σάς λένε ότι το παιδί σας είναι προβληματικό και “δεν το’ χει” με τον ρυθμό, ή απλά το ακούτε στο σπίτι να παίζει ασυναρτησίες ενώ προσπαθεί να διαβάσει, προβληματιστείτε σχετικά με την επιλογή του δασκάλου και δράσετε έγκαιρα. Είναι πολύ σοβαρό για να το αφήνετε…